5. Running Bycycle on 3D Arrays

Compute bycycle features for 3D organizations of timeseries.

Bycycle supports computing the features of 3D signals using BycycleGroup. Signals may be organized in a different ways, including (n_participants, n_channels, n_timepoints) or (n_channels, n_epochs, n_timepoints). The difference between these organizations is that continuity may be assumed across epochs, but not channels. The axis argument is used to specificy the axis to iterate over in parallel.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from neurodsp.sim import sim_combined

from bycycle import BycycleGroup
from bycycle.plts import plot_feature_categorical
from bycycle.utils import flatten_dfs

Example 1. The axis Argument

Here, we will show how the axis arguments works by iterating over slices of an 3D array. The axis argument be may specified as:

• axis=0 : Iterates over 2D slices along the zeroth dimension, (i.e. for each channel in (n_channels, n_epochs, n_timepoints)).

• axis=1 : Iterates over 2D slices along the first dimension (i.e. across flatten epochs in (n_epochs, n_timepoints)).

• axis=(0, 1) : Iterates over 1D slices along the zeroth and first dimension (i.e across each signal independently in (n_participants, n_channels, n_timepoints)).

arr = np.ones((2, 3, 4))

dim0_len = np.shape(arr)[0]
dim1_len = np.shape(arr)[1]

print("axis=0")
for dim0 in range(dim0_len):
    print(np.shape(arr[dim0]))

print("\naxis=1")
for dim1 in range(dim1_len):
    print(np.shape(arr[:, dim1]))

print("\naxis=(0, 1)")
for dim0 in range(dim0_len):
    for dim1 in range(dim1_len):
        print(np.shape(arr[dim0, dim1]))

axis=0
(3, 4)
(3, 4)

axis=1
(2, 4)
(2, 4)
(2, 4)

axis=(0, 1)
(4,)
(4,)
(4,)
(4,)
(4,)
(4,)

Example 2. 3D Array (n_channels, n_epochs, n_timepoints)

The features from a 3d array of (n_channels, n_epochs, n_timepoints) will be computed here. Bursting frequencies and rise-decay symmetry will be modulated across channels and epochs, respectively. The bursting frequencies and rise-decay symmetries will then be compared between the simulated parameters and bycycle’s calculation.

# Simulation settings
n_seconds = 10
fs = 500

f_range = (5, 15)

n_channels = 5
n_epochs = 10

# Define rdsym values for rest and task trials
rdsym_rest = 0.5
rdsym_task = 0.75

# Simulate a 3d timeseries
sim_components_rest = {'sim_powerlaw': dict(exponent=-2),
                       'sim_bursty_oscillation': dict(cycle='asine', rdsym=rdsym_rest)}

sim_components_task = {'sim_powerlaw': dict(exponent=-2),
                       'sim_bursty_oscillation': dict(cycle='asine', rdsym=rdsym_task)}

sigs_rest = np.zeros((n_channels, n_epochs, n_seconds*fs))
sigs_task = np.zeros((n_channels, n_epochs, n_seconds*fs))
freqs = np.linspace(5, 45, 5)

for ch_idx, freq in zip(range(n_channels), freqs):

    sim_components_rest['sim_bursty_oscillation']['freq'] = freq
    sim_components_task['sim_bursty_oscillation']['freq'] = freq

    for ep_idx in range(n_epochs):

        sigs_task[ch_idx][ep_idx] = sim_combined(n_seconds, fs, components=sim_components_task)
        sigs_rest[ch_idx][ep_idx] = sim_combined(n_seconds, fs, components=sim_components_rest)

# Compute features with an higher than default period consistency threshold.
#   This allows for more accurate estimates of burst frequency.
thresholds = dict(amp_fraction_threshold=0., amp_consistency_threshold=.5,
                  period_consistency_threshold=.9, monotonicity_threshold=.6,
                  min_n_cycles=3)

compute_kwargs = {'burst_method': 'cycles', 'threshold_kwargs': thresholds}

bg_rest = BycycleGroup(thresholds=thresholds)
bg_rest.fit(sigs_rest, fs, (1, 50), axis=0)

bg_task = BycycleGroup(thresholds=thresholds)
bg_task.fit(sigs_task, fs, (1, 50), axis=0)

df_rest = bg_rest.df_features
df_task = bg_task.df_features

# Merge dataframes, preserving channels
ch_labels = ["CH{ch_ind}".format(ch_ind=ch_ind) for ch_ind in range(n_channels)]

df_rest_ch = flatten_dfs(
    [pd.concat(df_rest[i]) for i in range(n_channels)], ch_labels, 'Channel'
)
df_task_ch = flatten_dfs(
    [pd.concat(df_task[i]) for i in range(n_channels)], ch_labels, 'Channel'
)

df_channels = pd.concat([df_rest_ch, df_task_ch])

# Merge across channels and epochs into a single dataframe
df_rest = flatten_dfs(df_rest, ['rest'] * n_channels * n_epochs, 'Epoch')
df_task = flatten_dfs(df_task, ['task'] * n_channels * n_epochs, 'Epoch')

df_epochs = pd.concat([df_rest, df_task])

# Limit to bursts
df_epochs = df_epochs[df_epochs['is_burst'] == True]
df_channels = df_channels[df_channels['is_burst'] == True]

# Plot estimated frequency
df_channels['freqs'] = fs / df_channels['period'].values

plot_feature_categorical(df_channels, 'freqs', 'Channel', ylabel='Burst Frequency',
                         xlabel=['CH00', 'CH01', 'CH02', 'CH03', 'CH04'])

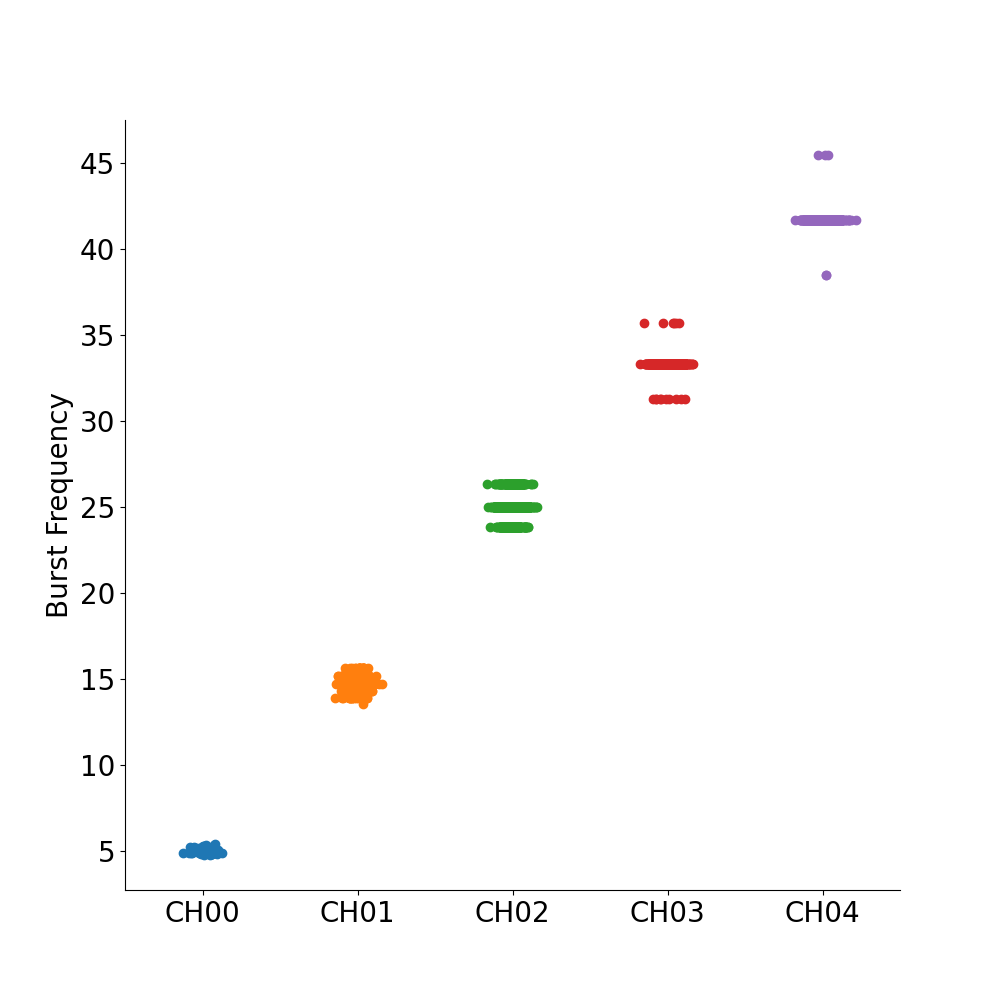
# Compare estimated frequency to simulatated frequency
freqs_est = df_channels.groupby('Channel').mean()['freqs'].values

df_freqs = pd.DataFrame()
df_freqs['Channel'] = ['CH_0{idx}'.format(idx=idx) for idx in range(n_channels)]
df_freqs['Simulated Freqs'] = freqs
df_freqs['Calculated Freqs'] = freqs_est
df_freqs['Error'] = np.abs(freqs - freqs_est)
df_freqs

	Channel	Simulated Freqs	Calculated Freqs	Error
0	CH_00	5.0	5.010568	0.010568
1	CH_01	15.0	14.704068	0.295932
2	CH_02	25.0	25.010205	0.010205
3	CH_03	35.0	33.328508	1.671492
4	CH_04	45.0	41.669018	3.330982

# See how well bycycle estimated each bursting cycle's rise-decay symmetry within epochs
rdsym_rest = df_epochs[df_epochs['Epoch'] == 'rest']['time_rdsym'].mean()
rdsym_task = df_epochs[df_epochs['Epoch'] == 'task']['time_rdsym'].mean()

df_rdsym = pd.DataFrame()
df_rdsym['Epoch Type'] = ['Fixation', 'Task']
df_rdsym['Simulated rdsym'] = [0.5, 0.75]

df_rdsym['Calculated rdsym'] = [rdsym_rest, rdsym_task]
df_rdsym['Error'] = np.abs(df_rdsym['Simulated rdsym'] - df_rdsym['Calculated rdsym'])
df_rdsym

	Epoch Type	Simulated rdsym	Calculated rdsym	Error
0	Fixation	0.50	0.508087	0.008087
1	Task	0.75	0.724396	0.025604